Data Augmentation——增加样本,并且控制模型复杂度
为什么data augmentation是理解为控制模型复杂度?
准确地说,我觉得data augmentation既不能简单地理解为增加training data,也不能简单地理解为控制模型复杂度,而是两种效果兼而有之。考虑图像识别里常用的改变aspect ratio做data augmentation的方法,生成的图像虽然和真实图像相似,但是并不是来自于data distribution,更不是它的i.i.d.抽样。而经典的supervised learning以及统计学习理论的基本假设就是训练集和测试集都是data distribution的i.i.d.抽样,所以这并不是经典意义上的增加training data。这些合成的training data的作用,流行的解释是“增强模型对某种变换的invariance”。这句话反过来说,就是机器学习里经常提到的“减少模型估计的variance”,也就是控制了模型的复杂度。需要注意的是,L2正则化、dropout等等也都是在控制模型复杂度,只不过它们没有考虑数据本身的分布,而data augmentation属于更加机智的控制模型复杂度的方法。
其实反过来看,L2正则化和dropout也各自等价于某种data augmentation。参考Vicinal Risk Minimization 和 1506.08700] Dropout as data augmentation
MixUp
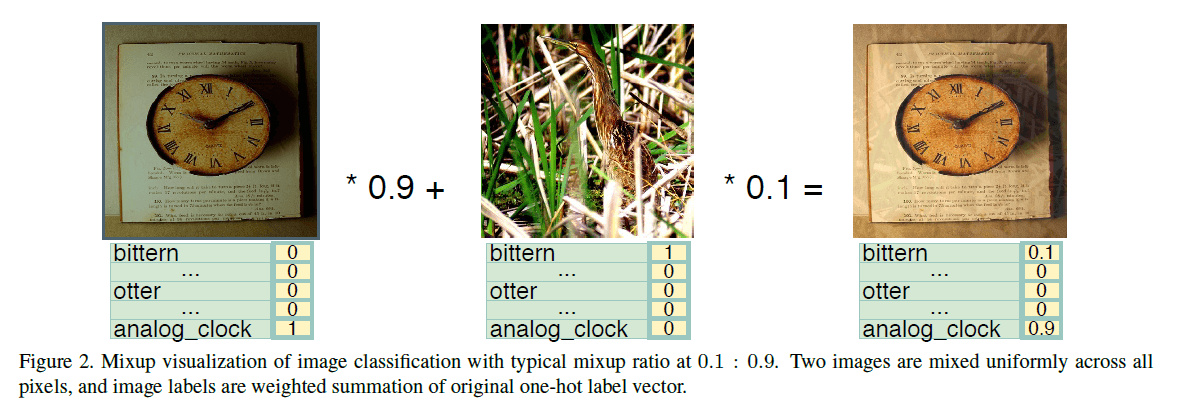
如上图所示,两幅图像相加后,结果已经不是一幅合理的图像了,这跟我们通常说的数据扩增完全不是一回事,为什么效果还会好?
让我们更数学化地描述这个问题,对于训练集对$(x_1,y_1), (x_2, y_2) … (x_n, y_n)$,我们希望找到一个模型ff,使得$y=f(x)$。对于图像分类等任务,鉴于问题本身具有较强的非线性,所以我们一般会用非常深的网络来拟合。然而,网络越深也意味着更加容易对训练集过拟合。
假设模型已经有能力预测$y_a=f(x_a),y_b=f(x_b)$了,那么对于mixup,它说这样还不够,模型还要同时对$\epsilon x_a+(1−\epsilon)x_b$输出$\epsilon y_a+(1−\epsilon)y_b$才行,也就是
$$
\epsilon y_a+(1-\epsilon)y_b=f(\epsilon x_a+(1-\epsilon)x_b)
$$
将$y_a, y_b$用$f(x_a), f(x_b)$代替,那么得到
$$
\epsilon f(x_a)+(1-\epsilon)f(x_b)=f(\epsilon f(x_a)+(1-\epsilon)f(x_b))
$$
这其实是一个函数方程,假如$\epsilon,x_a,x_b$都是任意的,那么上述函数方程的解就是“线性函数”,也就是说,只有线性函数才能使得上式恒成立,换句话说,mixup希望模型ff是一个线性函数。
我们知道,线性函数相当于没有加激活函数的单层神经网络,可以说是最简单的模型了,而我们实际建模时的模型则是深层的、具有大量参数的、具有强非线性能力的网络,而参数越多,越容易过拟合。这样一来,mixup的含义就很明显了:
mixup相当于一个正则项,它希望模型尽可能往线性函数靠近,也就是说,既保证模型预测尽可能准确,又让模型尽可能简单。
所以,mixup就是一个很强悍的模型过滤器:
在所有效果都差不多的模型中,选择最接近线性函数的那一个。
